Hello UOJ! 非常感谢 UOJ community for the great contests!!
- Problem: https://uoj.ac/contest/81/problem/793
- Editorial: https://qingyu.blog.uoj.ac/blog/8116
- Solution by zhoukangyang: https://www.cnblogs.com/zkyJuruo/p/17136175.html
I present a solution which is kind of a combination of the above two, so it might be essentially the same with them, but I hope it contains something valuable (e.g. easier to come up with).
First of all we need the very clever correspondence to the forest problem, described in 算法二点五 of the editorial.
To count the coloring ways, we can assign weight to each 道路 (thus to each edge), with the base answer
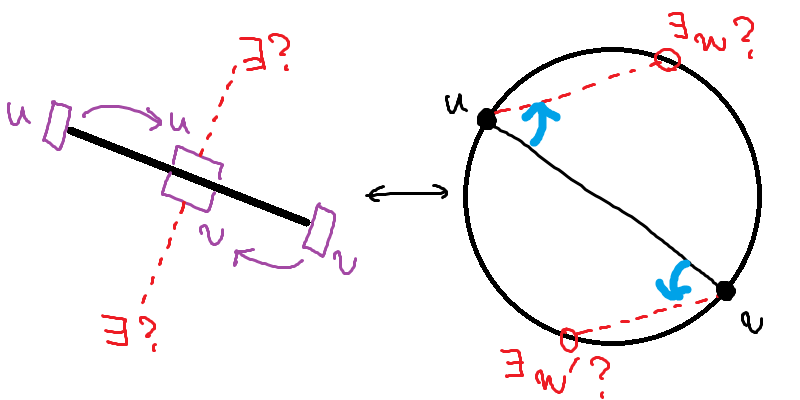
Now let's count the trees.
We define two GFs (with
For the whole tree, we can fix a root then its children are nothing or
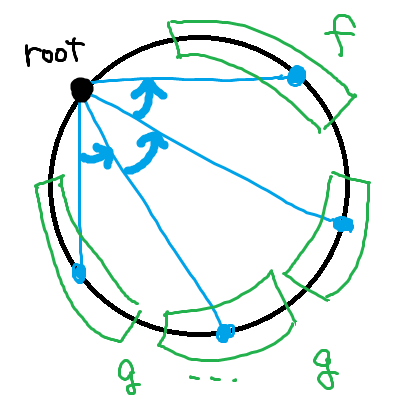
And we formulate the recurrence by noticing that the edge to the parent will separate the region into two parts:
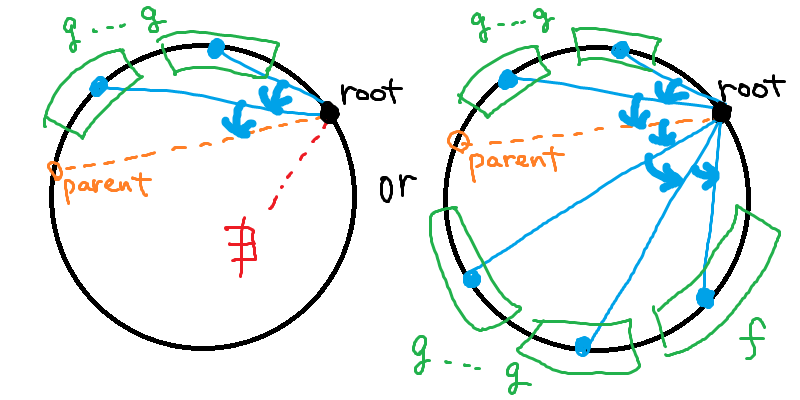
Solving the second one in
Then we can find
My submission: https://uoj.ac/submission/625385
I wonder if the equations above for
By the way, this solution is relatively simple if we just want to count the trees without considering the coloring (i.e. when

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号